Jak na TSP - Numerické myšlení - Číselné řady

Trocha teorie

Nejdříve něco málo z teorie, abyste se rychleji zorientovali. Pro úspěšné zvládnutí číselných řad Vám postačí několik málo jednoduchých pravidel.  

1. Číselné řady dělíme na jednoduché a složené

Jednoduché rozlišujeme na: Rostoucí: 1 4 7 10 ? Klesající: 10 8 6 4 ? Smíšené: 3 2 4 1 5 ? Složené se pak skládají z těchto jednoduchých číselných řad. Mohou být složené i třeba z 5ti číselných řad, ale v TSP MU se taková číselná řada zatím nikdy nevyskytla. Vždy byly složeny pouze z 2 číselných řad a s největší pravděpodobností tomu tak bude i nadále. Nejčastější variantou složených číselných řad je spojení jedné rostoucí a druhé klesající, ale mohou být i oboje klesající nebo rostoucí.

Klesající i rostoucí:

Dvě klesající:

Dvě rostoucí:

Zatímco s jednoduchou rostoucí a klesající nebývá problém. Rozlišit jednoduchou smíšenou a složenou z jedné rostoucí a jedné klesající může být pro někoho oříšek. Jak se ale tomuto problému vyhnout si ukážeme dále.

Takže pravidlo číslo 1: Nejdříve si musíme určit, o jaký typ číselné řady se jedná!

2. Mezi jednotlivými čísly bývají různé rozdíly.

Někdy přímo čísla číselné řady nám jasně říkají, které číslo bude následovat(1,2,3,4.. co bude asi následovat? :-) často takto bývají mocniny 2,3 a 5... takže číselá řada může být 2,4,8,16,32,64,128...) Co když nám ale samotná čísla číselné řady nijak nenapoví, jak má číselná řada pokračovat? Tuto informaci pak zjistíme až z rozdílu čísel nacházejících se v číselné řadě vedle sebe. Tyto rozdíly pak tvoří další číselnou řadu, nejčastěji se jedná o varianty, kdy jsou všechna čísla stejná,

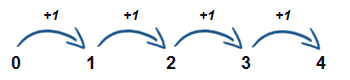
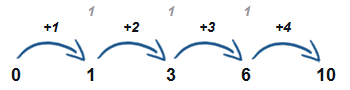
Čísla, která se zvětšují o stejná čísla (lineární řada- např. o 1 2 3 4)

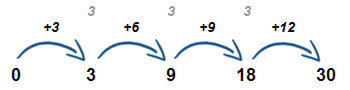
zvětšující se o násobky (1x3 2x3 3x3 4x3)

a násobné (a*1 b*2 c*3 d*4)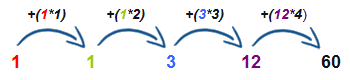

nebo mocninné (2⁰ 2¹ 2² 2³), (1² 2² 3² 4²), (1¹ 2² 3³ 4⁴)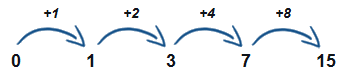

Zatímco první 3 mají lineární nárust hodnot, poslední 2 jej mají exponenciální. Toto Vám může napovědět o jaký typ se jedná již pohým pohledem na číselnou řadu. Pokud jsou první čísla malá a pak začnou prudce stoupat jedná se nejsíše o jednu z posledních 2 variant!

U smíšených číselných řad tvoří rozdíly jednu číselnou řadu, ale vždy je jedno číslo kladé a druhé záporné (1 -2 3 -4 5 -6), kdežto rozdíly složených číselných řad tvoří 2 na sobě nezávislé řady rozdílů. Pravidlo číslo 2: Určit rozdíly mezi čísly.  

3. A poslední bod, který již není ani pravidlem, ale spíše návodem jak postupovat.

Jak již bylo ukázáno výše. Je možné si dělat šipky mezi čísly a nad ně si psát rozdíly. Pokud se jedná o jednoduchou číselnou řadu, můžete si psát rozdíly přímo mezi čísla, ale u složených si dělejte obloučky, šipky nebo cokoli podobného, protože spojujete vždy čísla ob jedno. Můžete si dělat pro jednu číselnou řadu nahoře a pro druhou dole, nebo pokud budete mít po ruce více barev, odlište tyto číselné řady pomocí těchto barev. Jak jsem již zmiňoval, děláte rozdíly mezi čísly. Pokud se jedná o jednoduchou číselnou řadu, děláte rozdíly mezi čísly, které jsou vedle sebe, pokud se jedná o složenou, děláte rozdíly čísel ob jedno (protože se často jedná o 2 na sobě zcela nezávislé číselné řady).

Co ale dělat, když nevíte zda se jedná o jednoduchou smíšenou a nebo o složenou? Řešte ji tak jakoby šlo o složenou! Protože tento postup je sice trošičku složitější, ale funguje na obojí!

Doporučujeme si zopakovat malou a velkou násobilku a především mocniny 2, 3 a 5. Tato teorie Vám bude ale k ničemu, pokud si ji nevyzkoušíte v praxi. Takže hluboký nádech a hurá na video s příklady, nebo si příklady rovnou sami vyzkoušejte a pak jen zkontrolujte.